10月22日上午,統計與信息學院在線舉辦“非線性科學與數據科學”學術沙龍,邀請鄭州大學數學與統計學院院長薛波教授、中山大學數學學院吳朝中教授、寧波大學數學與統計學院李彪教授以及首都師範大學數學科學學院李春霞教授等知名專家作專題報告。統計與信息學院院長劉永輝,副院長王利娟、趙倩以及校內外專家🏄🏿♀️、學者、學生參加。沙龍由統計與信息學院趙海瓊教授主持🧗🏼♂️🦸🏽。

劉永輝代表學院致辭。他介紹了學院概況以及學院教師在非線性科學和數據科學研究方面取得的進展🧑🏻🦳🧃,感謝與會專家學者蒞臨沙龍傳經送寶。他表示🍣,非線性科學研究不僅具有重大的科學意義,而且對經濟和社會的發展也具有深遠的指導意義,隨著大數據時代的到來🕵🏼♀️,人工智能的蓬勃興起,對非線性科學🧾🧹、數據科學及其交叉研究將是新的機遇🐦⬛,期待校內外專家學者進一步加強交流合作🦻🏻,在探索大數據、深度學習等前沿科技的應用研究方面作出新的貢獻。
吳朝中以“On an extension of the Kadomtsev-Petviashvili hierarchy”為題作報告。他借助標量擬微分算子導出一個廣義的Kadomtsev-Petviashvili方程族,並進一步研究了其哈密頓結構、雙線性方程🦶🏽、附加對稱性和潛在的無限維Forbenius流形等性質🙆🏻♀️。上海交通大學朱佐農教授就Extended KP hierarchy、微分-差分模型以全離散模型等問題與吳朝中進行了交流探討。

李彪以“Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation”為題作報告。他介紹了基於物理信息的神經網絡構架在非線性動力學模型中的應用,提出了新的神經網絡算法GOPINNs,利用梯度統計技巧平衡損失函數中不同項之間的權重😌。他指出👩🎨🥅,該深度學習模型在預測有理波和孤子分形的動力學行為方面更有優勢👙。万泰娱乐統計與信息學院數據科學系系主任李睿副教授就模型的初邊值條件、魯棒性、數據量等問題與李彪進行了交流研討🥾。


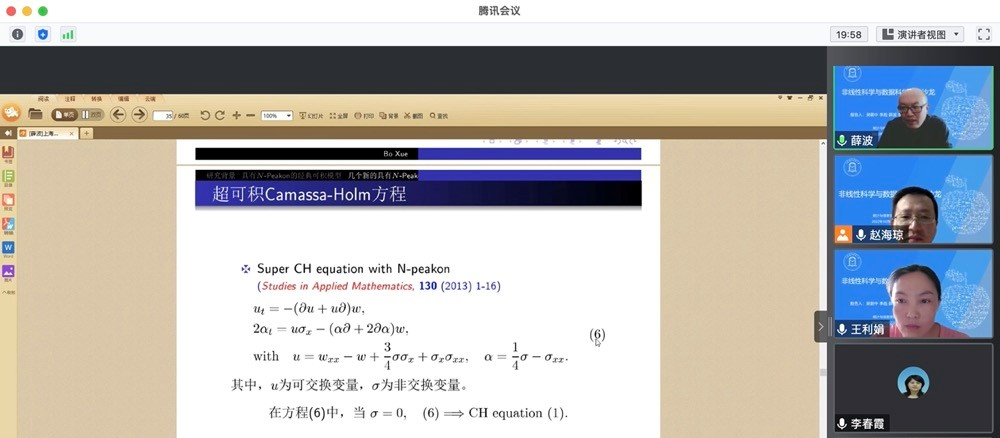
薛波以“Dynamical Models with N-peakons in Integrable Systems”為題作報告。他從孤立波的發現開始,介紹了可積系統領域發展過程中的一些重要成果🏃♀️,並以尖孤子理論這一熱點問題為基礎,介紹尖峰孤立子研究領域目前的最新進展。他指出🙎🏻♂️,在超可積模型中求解尖孤子計算復雜度較大,離散可積模型中尖孤子解等問題還需進一步研究。王利娟就經典解的存在性和尖孤子解的穩定性等問題與薛波進行了互動交流⚠。

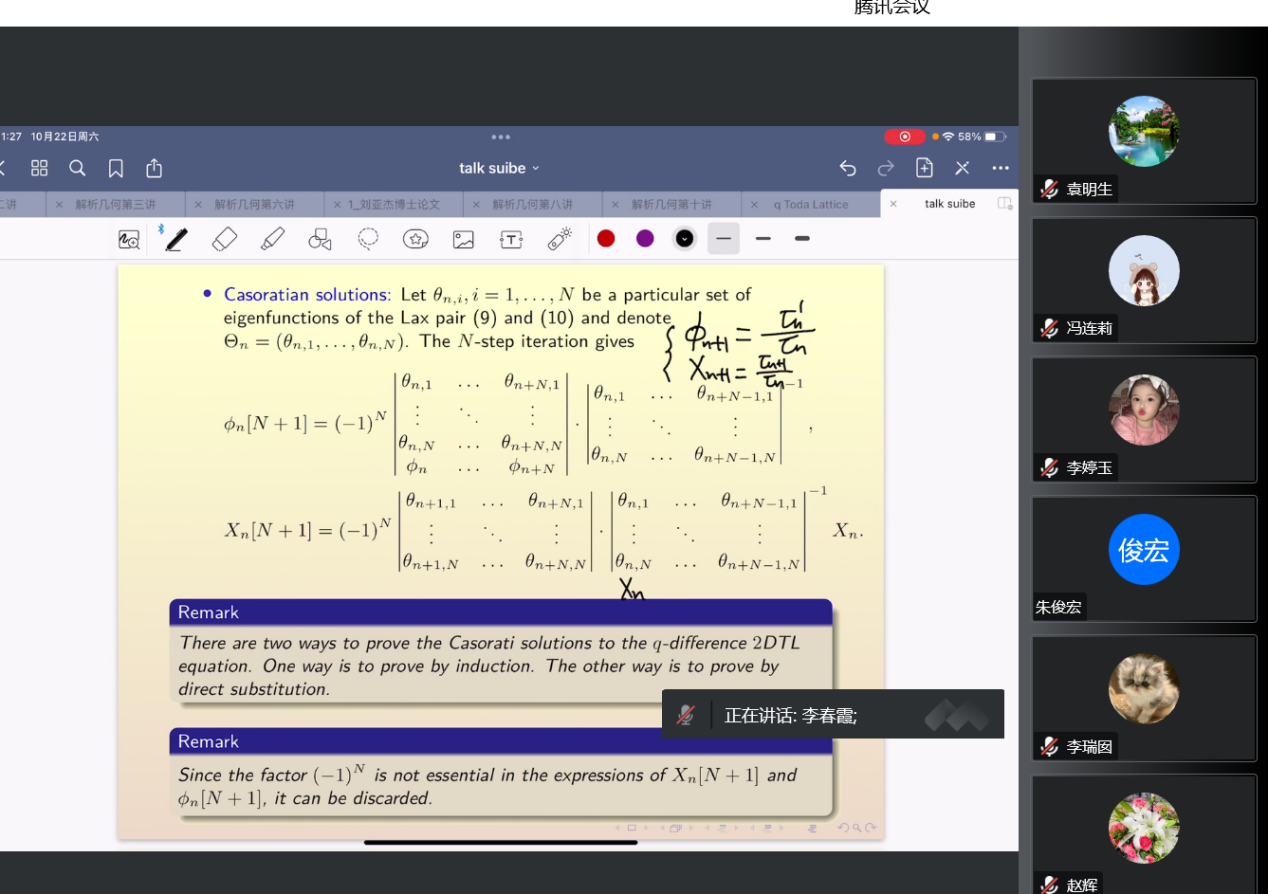
李春霞以“An insight into the q-difference two-dimensional Toda lattice equation, q-difference sine-Gordon equation and their integrability”為題作報告,給出q差分二維Toda晶格方程的廣義雙線性貝克隆變換和Lax對,進一步構造此模型的二元達布變換和格拉姆行列式解🫏。最後🦻🏿,考慮2周期約化,獲得q差分型的正弦戈登方程,修正q差分正弦戈登方程及其解。統計與信息學院應用數學系周統博士就q形變的可積系統理論、分數階可積模型,二元達布變換構造等內容與李春霞進行了探討。

在互動交流環節,與會師生們與專家們進行了熱烈討論。大家紛紛表示,通過本次沙龍💫,對非線性科學🪚、大數據、深度學習等學科前沿問題有了更深刻的了解和認識,受益匪淺。